Ein Unfall in Nordrussland und was Radioaktivitätsmesswerte bedeuten

Als ich meinen letzten Artikel angefangen habe, wollte ich die Geschichte über den Wodka aus Tschernobyl eigentlich nur als kleinen Aufhänger benutzen, um etwas über veröffentlichte Radioaktivitätsmesswerte und den dabei verwendeten Wust von Einheiten zu schreiben. Dann ist doch wieder eine typische Relativer-Quantenquark-Tirade daraus geworden, und die Erklärung der Einheiten wäre am Schluss einfach zu kurz gekommen – also habe ich da einen Folgeartikel angekündigt, den ich auch ganz schnell liefern will. Allerdings sind mir die tagesaktuellen Nachrichten auch da wieder zuvorgekommen: Aktuell häufen sich in den Medien Berichte über eine Freisetzung von radioaktiven Substanzen in Nordwestrussland. Da man das oft nicht so richtig einordnen kann, der Ort des Geschehens in Nyonoska liegt bei der roten Markierung, also ziemlich abgelegen, aber nicht wahnsinnig weit von Finnland entfernt.

Welche Gefährdung von den in den Artikeln genannten 1,78 bis 2 Mikrosievert gemessener Dosis pro Stunde über einen Tag hin ausgehen sollte, sollte man am Ende dieses Artikels ganz gut einschätzen können. Dass in der Region viel Gemüse aus dem eigenen Garten verzehrt wird, was, wie im letzten Artikel schon erklärt, die Bewertung beeinflussen sollte, halte ich dort für eher unwahrscheinlich. Die Bilder in russischen Medien sehen primär nach einem Großbrand eines ganz normalen Brennstoffs aus, aber wenn in diesem Brand irgendwo radioaktives Material freigesetzt wird, muss man natürlich schon davon ausgehen, dass das mit dem aufsteigenden Rauch einigermaßen großräumig verteilt wird. Videos auf Youtube, die den Vorfall zeigen sollen und eine riesige, ziemlich offensichtlich von konventionellem Brennstoff stammende, schwarze Rauchwolke zeigen, kursieren allerdings, wie Correctiv herausgefunden hat schon seit 2015 im Netz, so dass nähere Informationen weiterhin rar sind. 

Die Annahme derzeit ist, dass die Explosion bei Tests für den experimentellen russischen Flugkörper SSC-X-9 Skyfall (russische Bezeichnung 9M730 Буревестник „Sturmvogel“) ereignet haben dürfte. Das interessante an diesem Flugkörper, der nach amerikanischen Informationen allerdings bislang nur Abstürze produziert hat, ist, dass er über einen nuklearen Antrieb verfügen soll. Mit dem großen Energievorrat soll er nach einem russischen Video in der Lage sein, jedes Ziel auf der Welt im Tiefflug auf beliebigen Umwegen zu erreichen, was eine Abwehr erschweren soll. Das Video besteht allerdings zum größten Teil aus Computeranimationen – die echten Aufnahmen darin zeigen nur die Startphase, in der ziemlich offensichtlich eine konventionelle Feststoffrakete eingesetzt wird:

Als Physiker interessiert mich natürlich, wie so ein Antrieb funktionieren soll – und das müsste man auch wissen, um die Folgen eines Unfalls einschätzen zu können. Da muss ich zum Glück nicht wieder ausufern und mein eigentliches Thema wieder verschieben, denn dieser lange, aber wirklich gute Artikel mit dem Titel „The Best Bad Idea Ever?“ beleuchtet die wichtigsten technischen Aspekte und die Geschichte der Erforschung nuklear getriebener Flugzeuge und Flugkörper – und er erklärt, warum nie ein solches Flugzeug geflogen ist und wohl besser auch nicht sollte. In dem Artikel wird auch deutlich, was gemeint sein dürfte, wenn in diesem Kontext immer wieder mal eine ähnliche Technologie aus den USA erwähnt wird. Donald Trump twittert sogar, diese sei fortschrittlicher als die russische Skyfall, womit er offensichtlich die höhere Einsatzgeschwindigkeit der amerikanischen reaktorbeheizten Project-Pluto–Staustrahltriebwerke meint. Dabei fällt in der Regel unter den Tisch, dass diese amerikanischen Versuche vor 55 Jahren aufgegeben wurden…

Entscheidend für die Einschätzung eines Unfalls ist das enthaltene Material. Wenn man davon ausgeht, dass ein typischer Marschflugkörper im geraden Flug (abgeschätzt nach dem amerikanischen Tomahawk) etwa 3000 Newton Schub braucht und ungefähr 250 Meter pro Sekunde (900 km/h) schnell fliegt, dann leistet das Triebwerk etwa 750 Kilowatt. Rechnet man typische Wirkungsgrade dazu, dann müsste der Reaktor ungefähr ein Zehntel der Leistung des Forschungsreaktors München II haben, der durch Verwendung von hoch angereichertem Uran mit 8 kg Brennstoff auskommt. Der Reaktor des Flugkörpers müsste bei ähnlicher Masseneffizienz also ungefähr ein Kilogramm Uran enthalten. Sollte ein solcher Reaktor außer Kontrolle geraten und von seiner eigenen thermischen Leistung zerrissen werden, dann sollte sich das meiner Ansicht nach in der Umgebung durch weitaus mehr Fallout als die gemessenen 2 Mikrosievert pro Stunde äußern. Ich bin jedenfalls gespannt, was wir zu diesem Unfall noch erfahren werden. Im günstigsten Fall beendet er die Entwicklung dieser skurrilen Höllenmaschine, die heutzutage nun wirklich kein Mensch braucht.

Und damit zum eigentlich geplanten Thema, den Einheiten, die einem in Berichten über genau solche Ereignisse begegnen:

Im letzten Artikel habe ich nur die Einheiten Becquerel (Bq) und Sievert (Sv) verwendet, und das sind meines Erachtens auch die einzigen Einheiten zur Radioaktivität, die man in der Kommunikation mit Nichtphysikern verwenden sollte. Ich muss auch selbst jedesmal nachschlagen, wenn mir jemand Messwerte in antiquierten Einheiten wie Curie oder Milliröntgen um die Ohren haut, nur weil er zu faul ist, die Anzeige seines Messgeräts in aussagekräftige, zeitgemäße Einheiten umzurechnen. Becquerel und Sievert sind die einzigen Einheiten, die es sich meines Erachtens lohnt zu merken. Dazu lohnt es sich dann auch, sich ein paar Vergleichswerte zu merken, um Zahlen, die einem irgendwo begegnen, halbwegs einordnen zu können. Was die anderen Messwerte bedeuten und wie man sie umrechnet, möchte ich am Ende dieses Artikels kurz zusammenstellen.

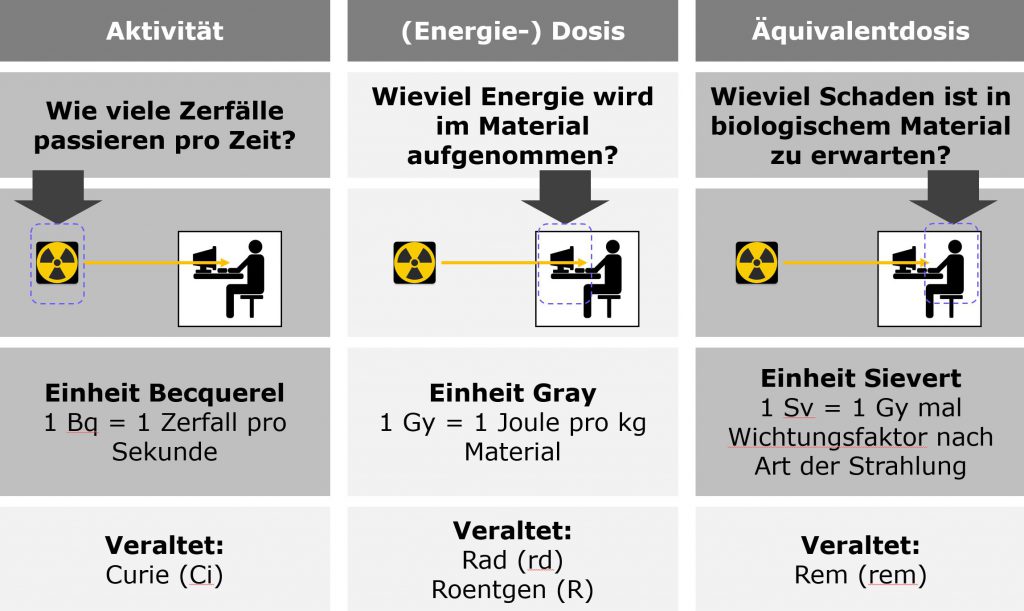
Zunächst einmal muss man sich bei einer Messung zur Radioaktivität fragen, was man überhaupt messen möchte. Grundsätzlich können Radioaktivitätsmessungen Antworten auf drei ganz unterschiedliche Fragen liefern:

1. Wieviel Radioaktivität ist da überhaupt? Besser wäre noch die Formulierung „wieviel Radioaktivität passiert da“, denn es geht ja schließlich um eine Aktivität. Anzugeben ist also, wie viele radioaktive Zerfälle (Umwandlungen eines Atomkerns in einen anderen unter Aussenden von Strahlung) in einem Material innerhalb eines gewissen Zeitraums passieren. Wählt man als Zeitraum eine Sekunde, dann kommt man genau auf die Einheit Becquerel (Bq), nämlich Zerfälle pro Sekunde. Wenn man nicht eine genau abgegrenzte Strahlenquelle, sondern ein in größerer Menge vorkommendes Material betrachtet, wird häufig die Aktivität pro Menge in Becquerel pro Kilogramm (Bq/kg) angegeben. Nun ist ein Atom in Größenordnungen unseres Alltags sehr klein, und entsprechend klein sind die bei Zerfällen freigesetzten Energiemengen. Beim Zerfall eines Kern des Wasserstoffisotops Tritium (das vor allem im Kühlwasser von Reaktoren entsteht) werden zum Beispiel 0,000000000000003 Joule Energie frei, davon etwa ein Drittel in Form von biologisch relevanter Betastrahlung (der Rest verbleibt im umgewandelten Atomkern oder verschwindet im nicht mehr nachweisbaren Neutrino auf Nimmerwiedersehen). Da man sich unter einem Joule auch nicht so viel vorstellen kann: Ein Joule ist etwa die Fallenergie von einem halben Pfund Butter, das aus 40 cm Höhe auf den Boden klatscht. Wenn man das halbe Pfund Butter hingegen aufisst, hat es einen Nährwert von etwa 8000 Kilojoule, also 8 Millionen Joule. Für eine physikalisch relevante Gesamtaktivität braucht man also schon einiges an Becquerel. Wenn man im Labor mit einer radioaktiven Quelle arbeitet, mit der man vernünftig etwas messen kann, ohne dass man im Umgang damit besondere Schutzausrüstung braucht, dann hat die in der Regel einige Kilobecquerel. Wenn man liest, dass beim Reaktorunfall von Three Mile Island (Harrisburg) 1979 geschätzte 1665 Terabecquerel (also Billionen Bq) Radioaktivität in Form von Gasen freigesetzt wurden, dann klingt das gigantisch. Zur Einordnung muss man sich allerdings klarmachen, dass auch ältere Bestrahlungsanlagen zur Krebstherapie in Krankenhäusern Kobalt-60-Quellen von einigen hundert Terabecquerel enthalten. Was eine Becquerel-Zahl für den Menschen bedeutet, hängt stark davon ab, um welche Art von Strahlung es sich handelt und wo die Zerfälle auftreten, insbesondere ob die Strahlenquelle sich außerhalb oder innerhalb des Körpers befindet und wie lange sie dort verbleibt. Mit dem 2015 in ein Überlaufbecken auf dem Werksgelände ausgetretenen Reaktorkühlwasser im Kraftwerk Temelin mit einer Tritium-Aktivität von 272 Becquerel pro Liter würde ich mir zum Beispiel bedenkenlos die Hände waschen oder auch darin baden. Trinken würde ich es dagegen nur im Notfall – allerdings immer noch lieber als zum Beispiel ungefiltertes Flusswasser. Gelangt radioaktives Material in den Körper, ist die Frage, wie lange es dort wo verbleibt. Bei der Ventilationsszintigraphie zur Untersuchung der Lunge atmet man 400 bis 800 Megabecquerel eines radioaktiven Edelgases ein. Da ein Edelgas mit praktisch nichts chemisch reagiert, wird es aber auch direkt wieder ausgeatmet. Die 55 Becquerel Tritiumaktivität aus einem Glas Temelin-Kühlwasser würden über den normalen Stoffwechsel des Körpers über die nächsten Tage wieder ausgeschieden. Jod-131, ein Produkt der Kernspaltung, ist der wichtigste Problemstoff in den ersten Wochen nach einem Reaktorunfall. Da bei den meisten Mitteleuropäern, die nicht regelmäßig Fisch essen oder mit Jodsalz kochen, der Jodbedarf des Körpers allenfalls knapp gedeckt ist, wird dieses radioaktive Jodisotop vom Körper gut aufgenommen, in der Schilddrüse eingelagert und kaum wieder ausgeschieden, sondern zerfällt mit einer Halbwertszeit von acht Tagen. Daher können auch relativ kleine Becquerel-Zahlen von Jod-131 im kleinen Volumen der Schilddrüse ein erhebliches Krebsrisiko verursachen. So ist der sonst seltene Schilddrüsenkrebs die einzige Krebsart, für die nach Tschernobyl in der allgemeinen Bevölkerung der Anliegerstaaten Ukraine und Weißrussland (außerhalb der an den Aufräumarbeiten beteiligten Liquidatoren) tatsächlich ein Anstieg erkennbar ist. Glücklicherweise ist Schilddrüsenkrebs zwar eine schwere Erkrankung, die erhebliche Einschränkungen der Lebensqualität mit sich bringt, verläuft aber nur in rund einem Zehntel der Fälle tödlich. Die Einlagerung von Jod in der Schilddrüse ist auch der Grund, weshalb man nach Reaktorunfällen bei gefährdeten Personen versucht, durch hochdosierte Jodtabletten ein Überangebot an nicht radioaktivem Jod zu schaffen, so dass ein möglichst großer Anteil des insgesamt verfügbaren (somit auch des radioaktiven) Jods wieder ausgeschieden wird. Radioaktive Problemstoffe, die sich über viele Jahre in den Knochen oder der Leber anreichern, sind die Brennstoffe Uran und Plutonium sowie die Spaltprodukte Cäsium-137 und Strontium-90. Da sie auch über viele Jahre nur zu kleinen Teilen zerfallen, können sich von diesen Stoffen selbst kleine Becquerel-Zahlen mit der Zeit zu erheblichen Belastungen aufsummieren. Das gilt insbesondere, wenn über einen langen Zeitraum die tägliche Nahrung belastet ist, was den im letzten Artikel erwähnten extrem niedrigen Strontium-90-Grenzwert in der Ukraine erklärt. Wegen dieser Unterschiede in der biologischen Relevanz der Aktivität unterschiedlicher Stoffe ist es auch so problematisch, wenn in dem in Fukushima aus den Reaktorruinen gepumpten Sickerwasser neben den rund einer Million Bq/l Tritium auch nach der Entsalzung noch Mengen von jeweils rund 100 Bq/l von anderen Isotopen gefunden werden. Ginge es nur um die insgesamt 760 Terabecquerel Tritiumaktivität des in Fukushima gespeicherten Wassers, dann könnte ich beim besten Willen nicht verstehen, warum man so zögert, diese einfach ins Meer abzuleiten: Tritium ist chemisch einfach Wasserstoff und reichert sich daher nirgends an, und verglichen mit der natürlichen Radioaktivität und selbst mit sonstigen menschlichen Einleitungen in die Weltmeere wäre diese Menge vernachlässigbar. Wenn man es aber tatsächlich nicht schafft, die Verunreinigungen mit radioaktiven Isotopen von Strontium, Cäsium oder anderen Substanzen, die sich in Fischen anreichern könnten, hinreichend gut zu entfernen, wäre das Verdampfen die teurere, aber sicherere Variante, weil diese Stoffe dabei in sehr kompakter Form zurückblieben. Die Aktivität in Becquerel ist also eigentlich nur in Verbindung mit anderen Informationen zur Beurteilung der Gefährlichkeit geeignet. Aussagekräftiger ist schon die folgende Frage:
2. Welche Strahlendosis wird von einem (lebenden) Material aufgenommen? Hier handelt es sich um eine absorbierte Energiemenge pro Material, gemessen in Joule pro Kilogramm, bezeichnet als die Einheit Gray (Gy). Die Dosis ist keine zeitbezogene Größe, kann sich also über Jahre aufsummieren. Will man die laufende Belastung an einem bestimmten Ort beschreiben, so verwendet man die Dosisleistung in (gegebenenfalls Milli- oder Mikro-) Gray pro Sekunde, Stunde oder Jahr. Geht es um Strahlungsschäden in technischen Geräten, zum Beispiel bei Halbleitern in Teilchendetektoren oder auf Satelliten, ist die Gesamtdosis über die Einsatzdauer die relevante Kennzahl. Bei lebendem Material, also auch in gesundheitlichen Fragen, ist die Situation komplexer. Für das Auftreten von akuter Strahlenkrankheit ist die innerhalb eines Zeitraums weniger Tage aufgenommene Dosis maßgebend. Über das Krebsrisiko und das Auftreten von Mutationen in der nächsten Generation entscheidet nach der bereits im letzten Artikel erwähnten Linearen Hypothese LNT ausschließlich die Gesamtdosis über die bisherige Lebenszeit ohne jegliche Heilungs- und Reparaturchancen. Wer sich mit der Frage beschäftigen will, wie realistisch das ist, dem empfehle ich den schon dort verlinkten Bericht des zuständigen wissenschaftlichen Ausschusses der Vereinten Nationen. Es wird aber, wie so oft in Gesundheitsfragen, noch komplizierter: Alle drei gesundheitlichen Folgen (Strahlenkrankheit, Krebs und Mutationen) entstehen durch Schäden des Erbguts, also der DNA, durch die absorbierte Energie der Strahlung. Die DNA bildet aber einen Doppelstrang, an dem die Erbinformation jeweils spiegelbildlich hinterlegt ist. Entsteht ein Schaden nur an einem Strang der DNA, so haben die zelleigenen Reparaturmechanismen wesentlich bessere Erfolgschancen, als wenn beide gegenüberliegenden Basen beschädigt oder gar beide Stränge durchtrennt sind. Es macht also einen Unterschied, ob die Energie der Strahlung an lauter isolierten Punkten durch das Gewebe verteilt wird oder ob elektrisch geladene Teilchen im Gewebe jeweils eine Spur der Verwüstung hinterlassen. Das führt zu der Frage:
3. Welcher Schaden entsteht durch die Strahlung in lebendem Gewebe? Diese Frage beantwortet die Äquivalentdosis in der Einheit Sievert (Sv). Sie errechnet sich einfach durch die Strahlungsdosis in Gray multipliziert mit einem Wichtungsfaktor, der sich nach der Art der Strahlung richtet. Für Teilchenstrahlung direkt aus einem Reaktor oder Beschleuniger sind diese Wichtungsfaktoren recht kompliziert, aber bei der Strahlung aus radioaktiven Zerfällen sind sie ganz einfach: Alphastrahlung, also die geladenen Heliumkerne, die nur von sehr schweren Kernen wie Uran oder Plutonium emittiert werden, hat den Wichtungsfaktor 20, sonstige radioaktive Strahlung den Wichtungsfaktor 1. Alphastrahlung kann die menschliche Haut nicht durchdringen und ist nur schädlich, wenn das radioaktive Material in den Körper gelangt. Daher ist für jede Strahlung, die von außen in den Körper hinein wirken kann, der Wichtungsfaktor 1 und damit die Äquivalentdosis in Sievert gleich der Strahlungsdosis in Gray. Neben den Wichtungsfaktoren für die Strahlungsart gibt es Gewebe-Wichtungsfaktoren, die eine Umrechnung zwischen den Äquivalentdosen einzelner Organe und der Ganzkörperdosis ermöglichen sollen. Da die Wichtungsfaktoren erkennbar den Charakter von Abschätzungen haben, hat es offensichtlich wenig Sinn, sich bei Äquivalentdosen Gedanken um die zweite oder dritte von Null abweichende Ziffer zu machen. Daher gibt es auch eine deutlich komplexere Berechnung der Äquivalentdosis nach sogenannten Qualitätsfaktoren, die für Teilchenstrahlung auf dem zu messenden Energieverlust beruhen, wenn man es wirklich genau wissen will. Für die Einschätzung von Risiken ist es aber eher entscheidend, die wievielte Ziffer einer Äquivalentdosis überhaupt von Null abweicht. Auch für die Äquivalentdosis wird häufig die Dosisleistung, zum Beispiel in Mikrosievert pro Stunde, angegeben.

Nachdem also die entscheidenden Fragen gestellt und grob charakterisiert sind, auf die Messwerte antworten sollen, können wir uns jetzt den einzelnen Einheiten zuwenden, die einem in den Medien begegnen können, wenn es um Radioaktivität geht – angefangen mit den beiden, die man tatsächlich kennen sollte und dafür jeweils ein paar Vergleichsgrößen zur Interpretation solcher Werte.

• Becquerel (Bq): Das Becquerel ist, wie oben erläutert, eine Einheit für die Aktivität und bezeichnet einen Zerfall pro Sekunde. Angegeben sind häufig auch Becquerel pro Menge eines Materials in Kilogramm oder Liter. Die Aktivitäten unterschiedlicher radioaktiver Substanzen sind hinsichtlich ihrer biologischen Relevanz nur bedingt vergleichbar. Ungefähre Vergleichswerte:
  • • 130 Bq: Natürliche Aktivität einer Banane.
    • 4000 Bq: Natürliche Aktivität im Körper eines Erwachsenen.
    • 1 GBq = 1.000.000.000 Bq: Größenordnung der Aktivität, die einem Patienten bei der Positronen-Emissions-Tomographie (PET) injiziert wird (Halbwertszeit maximal wenige Stunden).
    • 100 TBq = 100.000.000.000.000 Bq: Größenordnung der Aktivität in einer älteren Strahlungsquelle zur Krebstherapie.
    • 50.000 TBq = 50.000.000.000.000.000 Bq: Freisetzungsschwelle  zur höchsten Unfallstufe der IAEO-Skala für nukleare Ereignisse (Mayak 1957, Tschernobyl 1986, Fukushima 2011).
  • Sievert (Sv): Das Sievert ist eine Einheit für die Äquivalenzdosis, also die nach biologischer Wirkung gewichtete absorbierte Strahlendosis und hat die Dimension Energie pro Masse. Sie ist die beste bekannte Annäherung an den tatsächlich entstandenen Schaden. Im Gegensatz zum Becquerel ist das Sievert eine sehr große Einheit, so dass in der Regel Millisievert (mSv) oder Mikrosievert (μSv) angegeben werden. Ungefähre Vergleichswerte für die Ganzkörperdosis:
    • 50 μSv = 0,05 mSv: Ein Langstreckenflug.
    • 500 μSv/Jahr = 0,5 mSv/Jahr: Variation der natürlichen Radioaktivität zwischen unterschiedlichen Wohnorten in Deutschland.
    • 5 mSv/Jahr: Durchschnittliche Gesamtstrahlenbelastung in Deutschland (ca. 50% natürlich, 50% medizinisch).
    • 1.000 mSv = 1 Sv in kurzer Zeit: Einsetzen der akuten Strahlenkrankheit
    • 7.000 mSv = 7 Sv in kurzer Zeit: 100% tödlich.

Neben diesen beiden Einheiten, die man sinnvollerweise kennen sollte, um Informationen aus den Medien einordnen zu können, begegnen einem dort immer wieder auch andere Einheiten, die man nicht unbedingt kennen muss, deren Bedeutung und Umrechnung man aber bei Bedarf (z.B. hier) nachschlagen kann:

• Gray (Gy): Das Gray ist wie schon erwähnt die Standardeinheit für die Dosis, also die aufgenommene Strahlungsenergie pro Masse eines Materials, ohne Gewichtung der biologischen Wirksamkeit. Insofern ist sie zwar nicht veraltet, aber für gesundheitliche Fragen eher uninteressant, und die Werte sind häufig identisch mit denen in Sievert. Für Alphastrahlung aus Uran oder Plutonium gilt 1 Gy = 20 Sv, für alle andere Strahlung aus radioaktivem Material 1 Gy = 1 Sv.
• Rad (rd): Das Rad (radiation absorbed dose) ist eine seit mehr als 40 offiziell nicht mehr verwendete Einheit für die ungewichtete Dosis. Gerade Autoren mit, sagen wir, überschaubarer Sachkompetenz und vor allem aus dem medizinischen Sektor geben jedoch immer noch regelmäßig Messdaten in Rad an. Mitunter finden sich auch in derselben Tabelle, gedankenlos irgendwo abgeschrieben, untereinander Daten in Gray und in Rad ohne die wirklich triviale Umrechnung: 100 rd = 1 Gy; das entspricht 20 Sv für Alphastrahlung oder 1 Sv für sonstige Radioaktivität.
• Roentgen (R): Das Roentgen ist eine noch antiquiertere Einheit (es stammt aus der Frühzeit der Atomphysik und gilt schon seit 1953 als veraltet) und beschreibt eine Art Strahlungsintensität von Gamma- oder Röntgenstrahlung, die an einem Ort ankommt, gemessen an ihrer Fähigkeit, elektrische Ladungen aus Luftmolekülen herauszulösen. Das Problem dabei ist, dass die Umrechnung von Roentgen in eine Dosis vom Material abhängt, auf die die Strahlung auftrifft. Trotzdem stirbt auch das Roentgen in den Medien irgendwie nicht aus. In weichem Körpergewebe, das bei Strahlenschäden in der Regel interessiert, entsprechen 100 Roentgen knapp einem Sievert.
• Rem (rem): Mit dem Rem (Roentgen equivalent in man) wird es endgültig wirr, weil sich das Rem, wie aus dem Namen noch hervorgeht, ursprünglich von der Einheit Roentgen herleitete, es dann aber irgendwann als Äquivalentdosis zum Rad umdefiniert wurde. Dennoch erfreut sich das Rem vor allem in den USA bis heute großer Beliebtheit, wo man ja auch sonst der Meinung zu sein scheint, internationale Standardeinheiten machten das Leben zu einfach. Immerhin ist seit der Anlehnung an das Rad die Umrechnung überschaubar: 100 rem = 1 Sv.
• Curie (Ci): Das Curie ist eine Einheit für die Aktivität, die allen Ernstes 1910 noch unter Mitwirkung von Marie Curie selbst festgelegt wurde, und zwar als die Aktivität von einem Gramm Radium. Es wird seitdem hartnäckig immer noch benutzt, möglicherweise weil 10 Mikrocurie für eine radioaktive Quelle im Labor oder 45 Megacurie für die Jod-131-Freisetzung in Tschernobyl einfach weniger bedrohlich gigantisch klingen als die gleichen Werte in Becquerel. Leider gibt es für die Umrechnung keine einfach zu merkende Faustregel: 1 Curie entsprechen circa 37 Gigabecquerel…